KS2 Maths SATs Language Analysis

Mr Morgs’ next blog on how we can teach children to approach the language used in the reasoning papers in the KS2 SATs.

I intend on writing a series of blogs focused on the ‘literacy of numeracy’ because I believe that mathematical vocabulary is of the utmost importance to a child becoming a fluent and confident mathematician. Part 1 focuses on how we can teach children to approach the language used in the reasoning papers in the KS2 SATs. Whether it be their ability to understand a teacher’s spoken input or a written word problem, a child will not be able to comprehend in depth without secure understanding of vocabulary (in the same way a child would not be able to comprehend a text in literacy if there were too many unfamiliar words). Let me say from the outset: this does not mean using RUCSAC or getting children to circle words, it means explicit vocabulary teaching so that a child can see a word and instantly recognise its meaning, the context within which it manifests itself and the calculation that is required.

Currently, the maths SATs are split into three tests: an arithmetic test and two individual reasoning papers that follow a problem solving focus. This explicit separation of the tests should encourage us as teachers to teach towards the different tests separately, despite the fact the skills required for both are often inextricably linked. Indeed, the arithmetic paper holds no vocabulary that children must decipher and is instead purely number-based. But, the reasoning papers place a great emphasis on assessing a child’s knowledge of specific mathematical terms. Often the less fluent mathematicians struggle with the last few questions in a reasoning paper. In my experience, those children have often had no idea what the question is asking them to do because of their lack of mathematical vocabulary. We must approach these tests as if they were a reading test; children must have a depth of vocabulary if they are going to be able to approach them confidently and successfully. This can prove problematic for a number of reasons, as I have enumerated below.

A child could be tested on a variety of things:

1. their knowledge of synonyms usually linked to one of the four calculation types (take instead of subtract, product instead of answer, altogether rather than add)
2. their understanding of superlatives (biggest, largest, tallest, smallest)
3. words that can have different meanings outside of a mathematical context (round, product, factor, prime)
4. words other than superlatives that suggest comparison (between, more/less than, each, share, in order, sorting, put in the correct place)
5. their understanding of the difference between the right answer and the wrong answer (best estimate, explain why Jack is not correct, write the correct symbol in each box, circle the improper fraction that is equivalent)
6. Verbs implying mathematical meaning (remaining, left, combine, collect, spend)

NB: Any reference to 2015 in this blog is in reference to the Sample Papers released in 2015 so as not to confuse with the 2016 actual SATs papers.

To start, I will analyse the frequency of certain terms that I noticed appeared a lot. Naturally, if a child does not understand what a term means in one context, then their ability to understand it in another could be just as unlikely. Below is a frequency table to indicate how many times certain terms have been used from the 2015 sample papers onward. Obviously, there are other terms that have appeared more than once, but these were terms that I noticed were appearing enough to be significant to changing our classroom practice. I will now analyse each of these terms individually with implications for our class practice.

Analysis of frequently-used terms

‘Correct’ – naturally, it may be obvious why a term like this has appeared so much. However, there are some interesting points to be made about how it is used and what this means for our classroom practice. It has been used for children to identify the right answer by using the wrong one:

• 2015 Paper 2 Q6 – the watch is twelve minutes fast…what is the correct time?

Five times it has been used for children to demonstrate their reasoning for why somebody is correct or indeed incorrect:

• 2015 Paper 2 Q18 – Dev says “The pie charts show that more girls than boys liked milk chocolate best”. Dev is correct. Explain how you know.
• 2017 Paper 2 Q20 – Adam says, 0.25 is smaller than 2/5. Explain why he is correct.
• 2017 Paper 3 Q12 – Adam says, I have four times as many balloons as Chen. Explain why Adam is correct.
• 2018 Paper 2 Q9 – The cricket world cup has been held every four years since 1992. Adam is not correct. Explain how you know.
• 2018 Paper 3 Q14 – Jack says the triangle is equilateral. Explain why Jack is not correct.

Implications for class practice: in each of the statements above, children were required to either prove or disprove a statement. Therefore, we need to teach children to approach these questions so that they can argue for or against the statement being made. If Adam is correct in saying 0.25 is smaller than 2/5, then children must understand they have to prove this statement to be true. If Adam is not correct in saying that the Cricket World Cup has been held every 4 years since 1992, then children must be aware that they are looking for mathematical evidence to disprove his statement (i.e. a gap between two of the World Cups post 1992 where there has been a difference of either less or more than 4 years). Sounds obvious, doesn’t it? But how well do all children in our class answer these questions so that their answers are right beyond scrutiny?

Another instance of how the term ‘correct’ has been used is in questions where children must put in missing values in order to make a calculation correct:

• 2015 Paper 2 Q10 – write the two missing digits to make this long multiplication correct
• 2015 Paper 3 Q11 – write the four missing digits to make this addition correct
• 2016 Paper 2 Q3 – write the three missing digits to make this addition correct
• 2017 Paper 2 Q3 – write the missing numbers to make this multiplication grid correct
• 2017 Paper 3 Q1 – write the missing number to make this division correct
• 2018 Paper 3 Q4 – write the three missing digits to make this addition correct

Implications for class practice: children must remember that they will not be given transfers (carrying over) in these questions (as in the first three Qs above) and that they must put them in themselves. If missing ‘digits’ are required, children must remember to only put 1 digit from 0-9 in the box. Each of these questions also relies on the child’s ability to apply the inverse calculation to check their answer. Whether it is any of the four calculations mentioned in questions above, each time the child could have used the inverse to check the answer was correct. As in, when using the inverse, did they get the same missing digit that they have put in to solve the question? Just as with the reasoning questions containing the term ‘correct’, children can use their ability to prove and disprove to guarantee they arrive at a right answer. In order for their assumed missing digits to make this calculation correct, children must revisit it from start to finish after putting their answers in to check it works – they should be taught to go through the usual motions of that specific method (i.e. start from the right in column addition etc).
The term ‘correct’ may also apply to putting in missing values or symbols to make a statement correct

• 2016 Paper 2 Q7 – write the two missing values to make these equivalent fractions correct
• 2018 Paper 2 Q10 – write the correct symbol in each box the make the statements correct

Implications for class practice: the same as above. Check after putting something into a box if it does indeed make the statement ‘correct’.
Lastly, ‘correct’ has often been used in questions where children are given a value or symbol and they must put it somewhere to make something else correct:

• 2015 paper 3 Q13 – here are four fraction cards…use any three of the cards to make this correct <…<…<
• 2016 Paper 2 Q1 – Ali puts these five numbers in their correct places on a number line…write the number closest to 500
• 2016 Paper 2 Q5 – Write each number in its correct place on the diagram
• 2018 Paper 2 Q10 – Write the correct symbol in each box to make the statements correct
• 2018 Paper 2 Q16 – Tick the methods that are correct.

Implications for class practice: the overarching principle related to all of these correct questions? Children must be able to determine what is incorrect too. We can practise this daily by giving them conjecture to prove or disprove. This can be done with any topic! Sam believes…..Is he right? Why? Whenever possible, get children to write a sentence that includes a calculation in their answer to support it, as shown in these mark scheme answers from previous reasoning questions:

‘Equally’ – There have been three instances of the term ‘equally’ so far – all linked to division:

• 2015 Paper 2 Q16 – they share the cost equally
• 2017 Paper 3 Q2 – they share the money equally
• 2017 Paper 3 Q16 – Adam and Chen share the rest of the leaflets equally

Implications for class practice: Children need to be aware that when they see the term ‘equally’ that they are required to perform a division. They must understand that division is the splitting of a value into groups of equal size.

‘Equal’ – this has been used twice to demonstrate equal size in parts of shapes: shading in fractions of shapes and widths of rectangles. Perhaps more interestingly, it has been used the remaining three times to demonstrate an answer was needed, all to do with the recognition of place value:

• 2015 paper 3 Q12 – two decimal numbers add together to equal 1
• 2016 Paper 2 Q8 – circle two numbers that add together to equal 0.25
• 2016 Paper 3 Q19 – circle two numbers that multiply together to equal 1 million

Implications for class practice: In decimal questions like this, it would be wise to advise children to put in placeholders to help them see the place value more clearly. As in this question below from 2016, if children put a placeholder next to 0.2 to make it 0.20 then the answer may have been more obvious and may have prevented careless errors like circling 0.23 and 0.2  – children must also be aware that equal can be used as a synonym for answer.

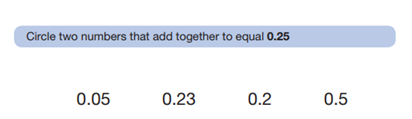
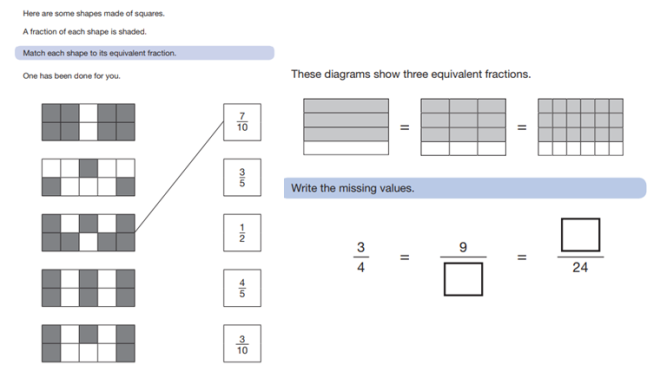
‘Equivalent’ – naturally, all questions involving ‘equivalent’ required children to demonstrate their knowledge of equivalent fractions through their times tables knowledge. Twice this has included children representing equivalent fractions in shaded shapes:

• 2015 Paper 2 Q4 – match each shape to its equivalent fraction
• 2018 Paper 2 Q4 – these diagrams show three equivalent fraction…write the missing values

The other three times required children to demonstrate their knowledge of how fractions can be equivalent to each other (both proper and improper) and the equivalence between fractions, decimals and percentages:

• 2016 Paper 2 Q7 – write the two missing values to make these equivalent fractions correct
• 2018 Paper 2 Q7 – tick the two numbers that are equivalent to 1/4
• 2018 Paper 2 Q13 – circle the improper fraction that is equivalent to 6 7/8

Implications for class practice: Children need to be confident in their understanding of equivalence between two forms. Whether that is between proper and improper fractions, or between fractions and decimals or percentages, the important knowledge required is times tables. If children are confident in their knowledge of times tables, the use of multiples and factors to find equivalence becomes a lot simpler. When asked to compare fractions with shapes, it is important to get children to write out the shaded part of shapes as fractions so that the equivalence becomes more obvious.

‘Missing’ – this term has come up with a variety of calculations attached – mostly attached to a division (5 times). More importantly, there were 10 instances when the term ‘missing’ should have indicated to children that they needed to use the inverse operation to solve.

• 2015 Paper 3 Q2 – write the missing number in the boxes
• 2015 Paper 3 Q14 – the number in a box is the product of the two numbers below it. Write the missing numbers
• 2016 Paper 2 Q18 – write the missing number
• 2016 Paper 3 Q1 – the numbers in this sequence increase by 14 each time. Write the missing numbers
• 2017 Paper 2 Q3 – write the missing numbers to make this multiplication grid correct
• 2017 Paper 2 Q5 – complete this table with missing numbers. One row has been done for you
• 2017 Paper 3 Q1 – write the missing number to make this division correct
• 2017 Paper 3 Q21 – the numbers in this sequence increase by the same amount each time write the missing numbers
• 2017 Paper 3 Q24 – calculate the missing length on cuboid B
• 2018 Paper 3 Q1 – write the missing numbers

Implications for class practice: children need to be taught to use inverse operations to be able to check their answers but also for the use of finding missing values. When the missing value is in the calculation and not the answer, like in 2016 Paper 2 Q16 and 2017 paper 3 Q1, children must learn to use the inverse to help them solve the calculation. NB: This is also an important skill for the arithmetic paper as missing values are appearing more frequently. This may also appear in context without the term ‘missing’ as shown below from 2015 Paper 3. The necessity for the inverse operation, however, is still present:

‘Missing’ – this has also come up in another context a few times. Children are asked to write in the missing digits for a column subtraction, addition or multiplication.

• 2015 Paper 2 Q10 – write the two missing digits to make this long multiplication correct
• 2015 Paper 3 Q11 – write the four missing digits to make this addition correct
• 2016 Paper 2 Q3 – write the three missing digits to make this addition correct
• 2018 Paper 3 Q4 – write the three missing digits to make this addition correct

Implications for class practice: these questions to do not put the transfers in for the children. Children must be taught to treat these like they would a normal written calculation, going through step by step and putting in the transfers themselves. This should be obvious to children as it might ask the child what you add to 9 to make 1; if a child is aware of transfers, they will know they are adding 2 to 9 and it is actually making 11 with a transfer into the next place value column (have a look at the question example below). It is important children work through some missing digit calculations in class to help them for these questions but also to cement their understanding of how these methods work. Another thing children could be taught is to write out the calculation to the side afterwards and see if they get the same answer with the digits they have put in – or even use the inverse to check their answer!

‘Cost’ – Naturally, this appears in the context of money every time. What is interesting with this term is that it often indicates a multi-step approach to solving the question. Even more intriguing is that one of those steps almost always included division. Below, I have listed all the ‘cost’ questions: next to each I have determined whether it needed a multi-step (MS) approach and followed this by the calculations needed to solve.

• 2015 Paper 2 Q8 – Cost = number of cakes x 20p + 15p for the bag. How much will a bag of 12 cakes cost? (MS – multiplication and addition) NB: the 2nd part to this question required the inverse as it gave children a cost and they had to work backwards!
• 2015 Paper 2 Q16 – Five children together buy one large pizza and three small pizzas. They share the cost equally. How much does each child pay? (MS – multiplication, addition and division)
• 2015 Paper 2 Q19 – One gram of gold costs £32.94. What is the cost of half a kilogram of gold? – (MS if children realised it would be easier to do 2 steps rather than one by doing x32.94 x 1000 and then divide it by 2)
• 2016 Paper 2 Q19 – Strawberries cost…Sugar costs…10 glass jars cost…Calculate the total cost to make 20 full jars of jam. (MS – multiplication and addition)
• 2018 Paper 2 Q18 – Jacob went to four concerts. Three of his tickets cost £5 each. The other ticket cost £7. What was the mean cost of the tickets? (MS – addition and division)

Implications for class practice: children must be confident in their ability to divide decimal amounts using short division. This includes any ‘cost’ that is presented to them in whole pounds like in 2018 Paper 2 Q18, which required children to divide £22 by 4 to find the mean. Those not fluent in their division of decimals presented an answer of £5 r2 rather than the correct £5.50. Children must also be aware that money questions involve a multi-step approach more often than not (normally the 2 mark ones!)
‘Cost’ – multi-step cost questions also appeared regularly asking for the price of one item:

• 2017 Paper 3 Q14 – 3 pineapples cost the same as 2 mangoes. One mango costs £1.35. How much does one pineapple cost? (MS – multiplication and division)
• 2017 Paper 2 Q19 – Amina posts three large letters. She pays with a £20 note. Her change is £14.96. What is the cost of posting one letter? (MS – subtraction and division)
• 2016 Paper 3 Q8 – Olivia buys three packets of nuts. She pays with a £2 coin. This is her change. What is the cost of one packet of nuts? (MS – subtraction and division)
• 2016 Paper 2 Q9 – 6 pencils costs £1.68. 3 pencils and 1 rubber cost £1.09. What is the cost of 1 rubber? (MS – division and subtraction)
• 2015 Paper 3 Q10 – A bag of 5 lemons costs £1. A bag of oranges costs £1.80. How much more does one orange cost than one lemon? (MS – division and subtraction)

Implications for class practice: children need to be taught that to find the cost for one individual item (among a group of the same item as seen above), that they must use division and divide by how many of the item there are. If the question is asking you to find the cost of a singular item from their change, you must subtract first before dividing. Children need to understand that change is a remaining amount after having paid, so it will always involve subtracting the cost from the money handed over – this is perhaps best explained with manipulatives and volunteers.
‘Each’ – searching for this term produced quite interesting results. ‘Each’ most likely puts an image of division or multiplication in our heads, but what do children think of when they hear it? In the majority of questions below, ‘each’ indicated that multiplication was the required calculation:

• 2015 Paper 2 Q2 – 4 children each take 7 sheets
• 2015 Paper 2 Q4 – A fraction of each shape is shaded. Match each shape to its equivalent fraction
• 2015 Paper 2 Q7 – in the circles, write a multiple that belongs to each set
• 2016 Paper 2 Q10 – each diagram below is divided into equal sections. Shade three-quarters of each diagram
• 2016 Paper 3 Q11 – each box contains 6 bags of marbles. Each bag contains 45 marbles
• 2017 Paper 2 Q11 – 20 minutes plus an extra 40 minutes for each kilogram
• 2017 Paper 2 Q13 – Jack buys 12 single stickers for 99p each
• 2017 Paper 2 Q18 – A cat sleeps for 12 hours each day…a koala sleeps for 18 hours each day
• 2017 Paper 3 Q2 – they get £16 each. How many friends in the group?
• 2017 Paper 3 Q16 – William and Ally take 450 leaflets each
• 2018 Paper 2 Q8 – each large box has 48 chocolates. Each small box has 24 chocolates
• 2018 Paper 2 Q18 – three of his tickets cost £5 each
• 2018 Paper 3 Q20 – Ken collects 2, 3 or 4 eggs each day from his hens

Of course, if it routinely involves the use of multiplication, then there was the odd occasion it was used for the inverse operation of division:

• 2017 Paper 2 Q19 – the postage costs the same for each letter…what is the cost of posting one letter?
• 2018 Paper 3 Q7 – each box holds six eggs. The farmer has 980 eggs to pack. How many boxes can the farmer fill using 980 eggs?

And the odd occasion where both multiplication and division were required – unsurprisingly, these were both worth 2 marks for the 2 operations:

• 2015 Paper 2 Q16 – Large pizzas cost £8.50 each. Small pizzas cost £6.75 each. Five children together buy one large pizza and three small pizzas. They share the cost equally. How much does each child pay?
• 2018 Paper 3 Q13 – A box contains 2.6 kg of washing powder. Jack uses 65 grams of powder for each wash. How many washes did Jack do?

‘Each’ also indicated just as frequently that children were required to give more than one answer. These questions also included the use of multiplication occasionally. If so, I have written (M) in brackets next to the question. There was only one use of ‘each’ throughout all the papers that only needed one answer:

• 2015 Paper 3 Q1 – write one number in each box (M)
• 2015 Paper 3 Q4 – write the name of each month where they collected more than £50
• 2015 Paper 3 Q6 – Use a card to complete each calculation (M)
• 2016 Paper 2 Q5 – write each number in its correct place on the diagram
• 2016 Paper 3 Q1 – the numbers in this sequence increase by 14 each time
• 2016 Paper 3 Q4 – each shape stands for a number. Work out the value of each shape (M)
• 2016 Paper 3 Q14 – complete each sentence using a number from the list below
• 2017 Paper 2 Q12 – tick each shape that has the same number of faces and vertices
• 2017 Paper 3 Q17 – in each box, circle the number that is greater
• 2017 Paper 3 Q21 – the numbers in this sequence increase by the same amount each time
• 2018 Paper 2 Q10 – write the correct symbol in each box to make the statements correct
• 2018 Paper 2 Q21 – she gives each shape a value…calculate the value of each shape (M)
• 2018 Paper 3 Q1 – the numbers in this sequence increase by the same amount each time (M – if children realised it was the 7x table but addition was more obvious)
• 2018 Paper 3 Q3 – write a digit in each box to show Layla’s number

Implications for classroom practice: children need to be taught that the term ‘each’ most likely indicates either multiplication or division, as it is splitting a value or values into groups. It is important to also show it to children in a sequence context (e.g. increases by 14 each time above) so that they understand how ‘each’ can be used in different questions.
‘Total’ – as expected, ‘total’ is used often to delineate an answer. More importantly, it almost always indicates the use of addition is needed at some point to solve the question:

• 2016 Paper 2 Q4 – What is the total of the numbers of people living in Formby and in Telford? (addition)
• 2016 Paper 2 Q19 – Calculate the total cost to make 20 jars full of jam. (multiply then addition)
• 2017 Paper 3 Q9 – What is the total number of hours for English on this timetable? (addition)
• 2017 Paper 3 Q18 – A square number and a prime number have a total of 22 (addition)
• 2018 Paper 3 Q6 – The total number of lions and tigers is 10 (addition)

Only one question didn’t require any addition. Although multiplication is repeated addition!

• 2016 Paper 3 Q11 – How many marbles does the shop order in total? (multiply)

Another point to make is that when ‘total’ was used alongside shape, as in the questions below, it meant children working backwards to find individual values:

• 2016 Paper 3 Q4 – Each shape stands for a number. Total 100…total 96…Work out the value of each shape.
• 2018 Paper 2 Q21 – Amina is making designs with two different shapes…total value is 147…total value is 111…calculate the value of each shape.

Implications for class practice: ‘total’ has appeared frequently in a 2 mark question format and once in a 3 mark question. Children must understand that, although commonly it indicates use of addition, it has been used for multiplication also. If ‘total’ appears alongside shape again, children must use the given ‘total’ to identify individual values that would then add up to make the ‘total’ provided.
‘Altogether’ – In each instance below, ‘altogether’ has been used to show a total, whether that be through combining two values or a single value:

• 2015 Paper 3 Q4 – How much money did they collect in February and March altogether?
• 2015 Paper 3 Q9 – What is the mass of these six coins altogether?
• 2017 Paper 2 Q1 – Altogether, how many children don’t walk to school?
• 2017 Paper 2 Q14 – Altogether, 12 seeds grew. (in the text before the question)
• 2018 Paper 2 Q8 – How many chocolates did Ken buy altogether?
• 2018 Paper 3 Q6 – There are 20 big cats in the zoo altogether. (in the text before the question)
• 2018 Paper 3 Q20 – In the first 20 days, Ken collects 57 eggs altogether. (in the text before the question)

Implications for class practice: ‘altogether’ has popped up in both the text before the question and in the question itself. Children need a solid understanding of what ‘altogether’ means so that they can understand it in both contexts. In each of the questions where ‘altogether’ was in the text before the question, it was establishing a value children had to remember in order to solve the question (i.e. knowing the 20 big cats made the entire pie chart, knowing Amina had 12 seeds grown for her ratio and that Ken already had 57 eggs so the following amount he collected had to be added to the 57 he already had). In the examples where ‘altogether’ was in the actual question, each time children were combining two or more values to find an answer (money in February and March; mass of three 10p coins and three 5p coins; children who don’t walk to school from Year 2 and Year 6; large boxes and small boxes of chocolate). If children can identify this difference in usage, answering the questions in which ‘altogether’ appears should become a lot easier.
‘Together’ – Similar to ‘altogether’, this term has been used to show a combination of two values. Except for the first question below, each time it has explicitly told children the calculation needed (add or multiply). In the first question, children had to make the link that buying them together meant adding the costs together:

• 2015 Paper 2 Q16 – Five children together buy one large pizza and three small pizzas
• 2015 Paper 3 Q12 – Two decimal numbers add together to equal 1
• 2016 Paper 2 Q8 – Circle two numbers that add together to equal 0.25
• 2016 Paper 3 Q19 – Circle two numbers that multiply together to equal 1 million
• 2017 Paper 3 Q3 – She multiplies them together

Implications for class practice: similar to that of ‘altogether’. The key point for children to remember with ‘together’ is that it means two values are being combined, whether that be adding or multiplying them is for the children to interpret in the individual context of the question.
‘How many’ – this is an interesting term that appeared 24 times across the 8 papers. There are a mixture of operations attached to them so I have put the operation needed in brackets after each question. There are five points to be made here. First, the vast majority of questions including the term ‘how many’ required children to perform multiplication or  division either to solve the entire question or for part of the question:

• 2015 Paper 2 Q8 – How many cakes are in the bag? (subtraction then division)
• 2015 Paper 2 Q20 – How many pages are there in Lara’s book? (division/multiplication – subtraction)
• 2016 Paper 2 Q11 – How many days does the packet of oats last? (multiplication and division)
• 2016 Paper 3 Q11 – How many marbles does the shop order in total? (multiplication)
• 2017 Paper 2 Q11 – How many minutes will it take to cook a 3kg chicken? (multiplication)
• 2017 Paper 2 Q14 – How many seeds did Amina plant? (multiplication)
• 2017 Paper 2 Q16 – How many degrees does Layla turn through her dive? (multiplication)
• 2017 Paper 3 Q2 – How many friends are in the group? (multiplication)
• 2017 Paper 3 Q16 – How many leaflets does Adam get? (multiplication and division)
• 2018 Paper 2 Q8 – How many chocolates did Ken buy altogether? (multiplication and addition)
• 2018 Paper 2 Q15 – How many melons does the supermarket sell? (multiplication)
• 2018 Paper 3 Q7a – How many boxes can the farmer fill using 980 eggs? (division)
• 2018 Paper 3 Q12 – How many times larger is the United Kingdom? (multiplication)
• 2018 Paper 3 Q13 – How many washes did Jack do? (multiplication and division)

The second point to make is that how many left questions always requires children to perform a subtraction at some point:

• 2015 Paper 2 Q2 – How many sheets of paper are left in the packet? (multiplication – subtraction)
• 2017 Paper 2 Q8 – How many toy cars were left in the toy shop at the end of June? (addition and subtraction)
• 2018 Paper 3 Q7b – How many eggs will be left over? (subtraction)
• 2018 Paper 3 Q11 – How many millilitres of water are left in Stefan’s bottle? (subtraction)
• 2018 Paper 3 Q16 – How many pages are left for Amina to read? (division and subtraction)

Third, the use of ‘how many’ alongside a graph, timetable or chart meant children could get a mark for simple retrieval of information – they had to interpret the data in front of them. Twice this also required children to perform a calculation also:

• 2016 Paper 3 Q9 – How many minutes does it take the 10:31 from Riverdale to reach Mott Haven? (retrieval)
• 2017 Paper 2 Q1a – How many children don’t walk to school? (retrieval)
• 2017 Paper 2 Q1b – How many more Year 6 children than Year 2 children walk to school? (retrieval and subtraction)
• 2017 Paper 3 Q4 – How many degrees warmer was it at 3pm than at 3am? (retrieval and subtraction)

Lastly, ‘how many’ followed by a comparative or superlative term could mean performing a subtraction was necessary:

• 2017 Paper 2 Q1b – How many more Year 6 children than Year 2 children walk to school? (retrieval and subtraction)
• 2017 Paper 3 Q4 – How many degrees warmer was it at 3pm than at 3am? (retrieval and subtraction)
• 2018 Paper 2 Q5 – How many degrees colder was Paris than Rome? (subtraction)

This question being the exception to the rule – however this question had the synonym ‘times’ which children should have realised meant to multiply:

• 2018 Paper 3 Q12 – How many times larger is the United Kingdom? (multiplication)

Implications for class practice:  children need to be taught to find the operation required using the term ‘how many’. Usually, this indicates the use of multiplication or division but not always. Children must be able to identify that ‘how many left’ questions always require subtraction and that if ‘how many’ is linked to a chart, graph or timetable etc that they must use a ruler and a pencil to circle the correct information they are being asked to retrieve (to avoid them putting the wrong answer in the box). Finally, children need to be aware that ‘how many’ followed by a comparative (more) or superlative (warmer, colder, larger) is always asking them to compare two values: this may mean subtraction is required but not always. Either way, children should identify more easily through their understanding of that language that it means a comparison is needed.
‘How much’ – this term has appeared 16 times across the papers and every time in either a money or measurement context. Here are several examples of this:

• 2015 Paper 2 Q8 – How much will a bag of 12 cakes cost? (money – multiplication and addition)
• 2015 Paper 2 Q16 – How much does each child pay? (money – multiplication and division)
• 2015 Paper 3 Q4 – How much money did they collect in February and March altogether? (money – addition)
• 2015 Paper 3 Q18 – How much chocolate should he use? (measurement – division)
• 2016 Paper 3 Q20 – How much money did Lara have to start with? (money – addition and multiplication)
• 2017 Paper 3 Q10 – How much milk is left? (measurement – subtraction)
• 2017 Paper 3 Q14 – How much does one pineapple cost? (money – multiplication and division)
• 2018 Paper 3 Q8 – How much does Jack spend on his new bike? (money – multiplication and division)

Similar to ‘how many’, when ‘how much’ appears with a comparative or superlative term after it, it is indicated the use of subtraction is required:

• 2015 Paper 3 Q10 – How much more does one orange cost than one lemon? (money – division and subtraction)
• 2015 Paper 3 Q19 – How much larger is the area of the football pitch than the area of the rugby pitch? (measurement – multiplication and subtraction)
• 2017 Paper 2 Q4 – How much higher is Mount Everest than the combined height of the other two mountains? (retrieval – measurement – subtraction)
• 2017 Paper 2 Q13 – How much more does Jack pay than Ally? (money – subtraction)
• 2017 Paper 3 Q5 – How much more money do they need to reach their target? (money – subtraction)

This was also true of the instances where the term ‘left’ appeared after ‘how much’:

• 2017 Paper 3 Q10 – How much milk is left? (measurement – subtraction)
• 2018 Paper 2 Q17 – How much orange juice is left over? (measurement – multiplication and subtraction)

Implications for class practice: the term ‘how much’ often presents itself in either a money or measurement context. It would be wise to introduce this into problems worked through as a class when learning these two topics. Children must also be confident in their ability to multiply or divide using decimal numbers, whether that be money (2015 Paper 2 Q16  – £6.75) or measurement (2018 Paper 2 Q17 – 0.225L). As was the case with ‘how many’, any instance of a comparative or superlative term following ‘how much’ indicates a comparison of values; with every instance so far showing a subtraction was needed. Just a side note on measurement questions while I remember. They always require children to convert between two units of measurement as they give two different units of measurement in each question (e.g. 2016 Paper 2 Q11 – 1.5kg and 50g / 2018 Paper 2 Q17 – 225ml and 8L). It is paramount children are confident in their knowledge of dividing and multiplying by 10, 100 and 1000. This is a necessary skill for the arithmetic paper too!

Comparative terms

These are terms that appear frequently in reasoning papers to indicate to children that comparison is needed at some point in the question for the answer to be found (e.g. Which cities have a population less than 50000 people? The child must find answers below 50000. They are comparing all the populations given with 50000 to see if they are lower or higher than that amount). Although this blog is only looking at language specifically, do not forget that comparison in mathematics can be shown through the use of symbols too with the use of inequality signs (< and >). These symbols have been used for 2 different questions (2015 Paper 3 Q13 and 2018 Paper 2 Q10) and both times children’s knowledge of them was assumed. Furthermore, the equals symbol (=) can be used for comparison to show that two statements or values are equivalent in value. Ensure children see this regularly!

‘Difference’ –  this term has always been used to show children that they need to perform a subtraction:

• 2015 Paper 2 Q3 – What was the difference between the temperature in Oslo and the temperature in Berlin?
• 2016 Paper 2 Q4 – What is the difference between the numbers of people living in Bedford and in Dover?
• 2016 Paper 3 Q2 – What is the difference between the temperature on 1st January and the temperature on 8th January?

Implication for class practice: children need to understand that a difference is a comparison of a larger amount and a smaller amount through subtraction. Subtraction has the root word ‘tract’, meaning to ‘drag or pull from’- this can help children to remember to put the bigger number on top in the column method and take from it. Furthermore, notice how in each context above children had to interpret data from a table too. It would be wise to combine subtraction with data interpretation in your practice questions in class.
‘Different’ – has always been used for comparison. In each instance, children had to notice the value of one thing before finding the value of another:

• 2016 Paper 3 Q10 – Write the letter of the cuboid that has a different volume from Emma’s cuboid
• 2016 Paper 3 Q17 – Four of the triangles have the same area. Which triangle has a different area?
• 2018 Paper 2 Q21 – Amina is making designs with two different shapes…calculate the value of each shape.

In the most recent example (Q21 last year), the word ‘different’ would have helped children to notice that not only were the shapes ‘different’, but so too were their values. By focusing on the term ‘different’, children should have been able to establish that the shapes were different by having one less hexagon and the values were different by a gap of 36. By seeing the relationship between the two, the question becomes a lot easier to solve.

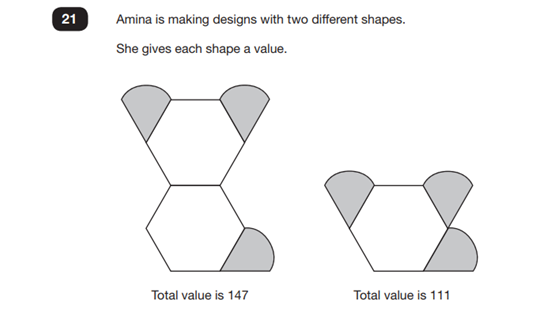
Implications for class practice: children must understand that if they see the term ‘different’, it means they must compare two things from the question (e.g. shapes, values) and see how they are similar or different. This could be a difference numerically or in size or shape.
‘Than’ – unsurprisingly, ‘than’ was always used to show comparison as shown below:

• 2015 Paper 3 Q10 – How much more does one orange cost than one lemon?
• 2015 Paper 3 Q19 – How much larger is the area of the football pitch than the area of the rugby pitch?
• 2017 Paper 2 Q13 – How much more does Jack pay than Ally?
• 2017 Paper 3 Q20 – A rectangular tile is 3 cm longer and 2 cm narrower than the square tile.
• 2018 Paper 3 Q3 – 2 so that it has a higher value than any of the other digits
• 2018 Paper 3 Q12 – The area of the United Kingdom is larger than the area of Jamaica.

However, there is an interesting point to be made. When ‘than’ appeared in a question context including data (temperatures, money raised on a graph, animals in a zoo, number of children walking to school), the children simply had to interpret the data to either prove a statement right:

• 2015 Paper 2 Q18 – The pie charts show that more girls than boys liked milk chocolate best…Explain how you know.
• 2015 Paper 3 Q4 – Write the name of each month where they collected more than £50
• 2018 Paper 3 Q6 – Tick the statements that are right…there are more cheetahs than jaguars...there are more than 5 jaguars.

Or interpret the data to be able to perform the calculation that the question wanted. Only once children had identified the necessary data could they perform the necessary calculations needed below:

• 2015 Paper 2 Q3 – Which city was 4 degrees warmer than Kiev?
• 2016 Paper 3 Q2 – On 22nd January the temperature was 7 degrees lower than on 15th January. What was the temperature on 22nd January?
• 2017 Paper 2 Q1 – How many more Year 6 children than Year 2 children walk to school?
• 2017 Paper 2 Q4 – How much higher is Mount Everest than the combined height of the other two mountains?
• 2017 Paper 3 Q4a – How many degrees warmer was it at 3pm than at 3am?
• 2017 Paper 3 Q4b – At 6 pm the temperature was 4 degrees lower than at 3pm. What was the temperature at 6pm?
• 2018 Paper 2 Q5a – At midnight, how many degrees colder was Paris than Rome?
• 2018 Paper 2 Q5b – Which city was 6 degrees colder at midnight than at midday?

Another conclusion that can be made is to do with the term ‘than’ being used to demonstrate that a value is less or greater than. In these instances, children should understand that their answer falls within a certain range (i.e. less than 100 means their answer cannot be 100 or above).

• 2015 Paper 2 Q1 –                  is 20 more than 237
• 2015 Paper 3 Q16 – Lara chooses a number less than 100
• 2016 Paper 2 Q14 – Write all the common multiples of 3 and 8 that are less than 50
• 2016 Paper 2 Q16a – Write the number that is five less than ten million
• 2016 Paper 2 Q16b – Write the number that is one hundred thousand less than six million
• 2016 Paper 3 Q13 – Lara chooses a number less than 20
• 2017 Paper 2 Q2 – Circle the number that is 10 times greater than nine hundred and seven.
• 2017 Paper 2 Q20 – 25 is smaller than 2/5

Implications for classroom practice: it is important to remember that ‘than’ can also be indicated through use of the inequality signs, also known as greater than < and less than > symbols. Children need to be taught that ‘than’ is used for comparison and that they must compare two or more values when they see the term. When learning about data interpretation, it is important for children to attempt questions that ask them which values are less or greater than each other (i.e. which subject do children enjoy more than English in the graph?) Again, any questions including data interpretation should encourage children to use a pencil and a ruler to single out the data they are being asked about, rather than accidentally looking at the wrong column or wrong bar in a bar graph etc. Finally, children must be aware that if the question states an answer is less or more than a certain value (e.g. 2106 Paper 3 Q13 – Lara chooses a number less than 20), then any answer that outside of the given range is impossible (i.e. any answer in this case that is 20 or above).
‘Less’ – this term has only occurred a few times and in two different ways. First of all, to show that an answer was below a certain amount:

• 2015 Paper 3 Q16 – Lara chooses a number less than 100
• 2016 Paper 3 Q13 – Lara chooses a number less than 20
• 2016 Paper 2 Q14 – Write all the common multiples of 3 and 8 that are less than 50

Secondly, to show an answer is below a certain amount but through a subtraction as the choice of operation:

• 2016 Paper 2 Q16 – Write the number that is five less than ten million
• 2016 Paper 2 Q16 – Write the number that is one hundred thousand less than six million.

Implications for class practice: note what has already been said about terms of comparison; children need to remember their answer must meet the requirements given but also that less can indicate use of subtraction. I like to teach children this through the suffix ‘less’ which means without (e.g. heartless, careless). This helps them to remember a subtraction is needed, because now a number is going to be without a value it originally had.
‘More’ –  this has been used in questions that have a predetermined value from which the children have to base their answer. In each of the cases below, their given answer just had to satisfy the value given by being higher than it:

• 2018 Paper 2 Q6 – There are more cheetahs than jaguars… There are more than 5 jaguars (tick if correct)
• 2015 Paper 2 Q18 – “The pie charts show that more girls than boys liked milk chocolate best.” Explain how you know.
• 2015 Paper 3 Q4 – Write the name of each month where they collected more than £50

Three times it has been used to demonstrate addition was required:

• 2015 Paper 2 Q1 – 180 is 20 more than 160… is 20 more than 237
• 2017 Paper 2 Q5 – 1,000 more
• 2017 Paper 2 Q8 – 8,728 more toy cars were delivered

Perhaps the most important point to note is that when the term ‘more’ was coupled with either ‘how much’ or ‘how many’, it always indicated a subtraction was needed in order to find a difference between two values:

• 2015 Paper 3 Q10 – How much more does one orange cost than one lemon?
• 2017 Paper 2 Q1 – How many more Year 6 children than Year 2 children walk to school?
• 2017 Paper 2 Q13 – How much more does Jack pay than Ally?
• 2017 Paper 3 Q5 – How much more money do they need to reach their target?

Implications for class practice: the significant point for classroom practice here is that ‘more’ does not always indicate an addition like most children might assume. In every instance above, ‘more’ indicates one value being higher than another – this is the key thing to teach children. However, this could mean adding ‘more’ to make a value bigger or finding how much or many ‘more’ a value is and therefore using subtraction. Children need to see the term in both contexts to fully understand its use. Children must understand that ‘how many more’ or ‘how much more’ is trying to find a difference in values, by seeing which value is bigger and by how much; in every case, a subtraction is needed.

Superlative Terms

What is immediately clear from the table above is that, although specific superlatives may not appear every year, the use of superlatives is prevalent throughout every set of reasoning papers each year (with an average of 10 being used yearly). In fact, although specific ones aren’t recurring often, it shows that the test makers are varying their use of superlatives as you can see with ‘colder’ and ‘greatest’, which both appeared for the first time last year. It is important that children are exposed to as wide a variety of superlatives as possible to avoid any confusion in understanding the question. In both instances that ‘greatest’ appeared last year, both questions were worth 2 marks and the term ‘greatest’ was used in the actual question:

• 2018 Paper 3 Q15 – What is the greatest number of colours she can have in the design?
• 2018 Paper 3 Q20 – What is the greatest number of eggs Ken can collect in March?

If children didn’t understand the term, then they lost out on 4 marks instantly. I remember the egg question being particularly tricky in my class even among the greater depth children!
As each superlative doesn’t appear too frequently I will group all the implications for class practice below in bullet point form:

• ‘warmer’ and ‘colder’ and ‘lower’ – in each instance of their use, the context of the question was temperature. Perhaps less obviously, children needed to perform a subtraction to find a difference between two values. This can be tricky because it can include both positive and negative values so maybe the use of numberline should be encouraged.
• ‘nearest’ – this has only ever appeared in a rounding context. Make sure children are confident in their ability to round well because in the three years it has popped up, it has been worth 2 marks each time. Ensure children hear the term ‘nearest’ regularly when teaching rounding.
• ‘closest’ and ‘furthest’ – each of these has only appeared once, however it is important children understand this is testing their understanding of place value if it does pop up again. Children could label the values given with their place value columns or simply draw a place value grid and put all the numbers into it.
• ‘larger’ – both times this has been seen the use of multiplication was needed
• ‘smallest’ – each of the times this has appeared, children had to order values from ‘smallest’ to largest. Twice this has been decimals with different amounts of decimal places and once as fractions with different denominators. Children must understand that ‘smallest’ means finding the value that is the least biggest in comparison to the others, whatever representation the value is in.
• ‘earliest’ and ‘latest’ – these have obviously only appeared in the context of time – make sure children hear them in your lessons on time!

Although not always true, superlatives ending in ‘est’ normally indicate children need to simply identify a value and could be solved mentally without any written method or long working out:

• 2015 Paper 2 Q9a – Measure the shortest side accurately, in centimetres (sides already provided simply had to identify and measure)
• 2015 Paper 2 Q9b – Measure the largest angle (angles already provided simply had to identify and measure)
• 2016 Paper 2 Q1a – Write the number closest to 500 (numbers already provided)
• 2016 Paper 2 Q1b – Write the number furthest from 500 (numbers already provided)
• 2016 Paper 2Q2 – Put these houses in order of price starting with the lowest (prices already provided)
• 2016 Paper 3 Q9 – What is the earliest time he can reach Tremont on the bus? (times already provided)
• 2017 Paper 3 Q6 – Circle the latest time that William can leave London. (times already provided)

This is also true of the rounding questions as long as children are confident in their place value:

• 2015 Paper 2 Q14 – Round 124,531 to the nearest 10,000…1,000…100
• 2016 Paper 3 Q15 – Complete this table by rounding numbers to the nearest hundred
• 2017 Paper 2 Q10 – Round 84,516 to the nearest..100…1,000
• 2017 Paper 3 Q19 – He rounds his answer to the nearest 10

These two questions were the exception where children did need to perform calculations without being able to solve mentally. Both from last year and both with the use of the same term:

• 2018 Paper 3 Q15 – What is the greatest number of colours she can have in the design?
• 2018 Paper 3 Q20 – What is the greatest number of eggs Ken can collect in March?

Implications for class practice: it would be wise to inform children that an ‘est’ superlative often involves little working out and simply identifying a value provided. As long as children are aware of this, it may make these questions easier for them. We can teach children to search for this in context and therefore help them to approach these questions in a simpler manner.
Conversely, superlatives ending in ‘er’ normally (not always) indicated that working out was necessary in order to find the answer for those less fluent. Of course, if children were fluent and confident in their knowledge, some of these could be done mentally. I have indicated the questions that could be done mentally by putting (M) after each of those questions. However, I have ultimately decided to keep them all in the same list as a lot of children who aren’t fluent would have used working out to solve these questions:

• 2015 Paper 2 Q3 – Which city was 4 degrees warmer than Kiev? (M)
• 2015 Paper 3 Q19 – How much larger is the area of the football pitch than the area of the rugby pitch?
• 2016 Paper 3 Q2 – On 22nd January the temperature was 7 degrees lower than on 15th January. What was the temperature on 22nd January? (M)
• 2017 Paper 2 Q2 – Circle the number that is 10 times greater than nine hundred and seven. (M)
• 2017 Paper 2 Q4 – How much higher is Mount Everest than the combined height of the other two mountains?
• 2017 Paper 2 Q20 – Adam says 0.25 is smaller than 2/5. Explain why he is correct.
• 2017 Paper 3 Q4a – How many degrees warmer was it at 3pm than at 3am? (M)
• 2017 Paper 3 Q4b – At 6 pm the temperature was 4 degrees lower than at 3 pm. What was the temperature at 6 pm? (M)
• 2017 Paper 3 Q17 – In each box, circle the number that is greater. (M)
• 2017 Paper 3 Q20 – A square tile measures 20 cm by 20 cm. A rectangular tile is 3 cm longer and 2 cm narrower than the square tile. What is the difference in area between the two tiles?
• 2018 Paper 2 Q5a – At midnight, how many degrees colder was Paris than Rome? (M)
• 2018 Paper 2 Q5b – Which city was 6 degrees colder at midnight than at midday? (M)
• 2018 Paper 2 Q12 – How many times larger is the United Kingdom? (M)
• 2018 Paper 3 Q3 – 2 so that it has a higher value than any of the other digits…the remaining two digits so that 7 has the higher value. (M)

Synonyms

There is no ‘implications for class practice’ section here as the implications for our teaching practice is obvious: children need to be exposed to as many synonyms for the four different operations as possible because the reasoning tests always utilise a wide variety of synonyms. We must remember as teachers that some terms can be used for more than one operation and not take it for granted that children know this as well as we do.
This table only includes language that is explicitly clear in demonstrating the operation. It therefore avoids questions like this that are not explicitly clear for children in which operations they should use:

NB: Where possible, this table only includes synonyms and not phrases or whole sentences that may also indicate operation. Emboldened words are terms that could be used for more than one operation or require two operations for solving (i.e. mean).

It is also worth mentioning that synonyms for ‘answer’ are often utilised (product, result, equal, remaining, left, left over). Children should also be aware of these.

The importance of past papers in teaching vocabulary and comprehension

No doubt using past papers is something all Year 6 teachers do. Rightfully so, it allows us to assess our classes and get a rough idea of what topics they struggle with and even the scores they might get on the day. But perhaps lesser known – and this is something that really benefitted my class last year during revision sessions – is that questions are often recreated in very similar (or exactly the same) contexts year on year. For this reason, it is very important that children see past questions regularly. Below, I have put questions from previous years that were similar to each other:

2015 Paper 2 Q4 and 2018 Paper 2 Q4

2016 Paper 2 Q11 and 2018 Paper 3 Q13

2018 Paper 3 Q1 and 2016 Paper 3 Q1 and 2017 Paper 3 Q21

2015 Paper 3 Q21 and 2016 Paper 3 Q13

2015 Paper 2 Q8 and 2018 Paper 3 Q15 and 2017 Paper 2 Q11

note that the 2nd part to all of these questions gave children an answer (cost, price and cooking time) with which they had to work backwards from using the inverse.

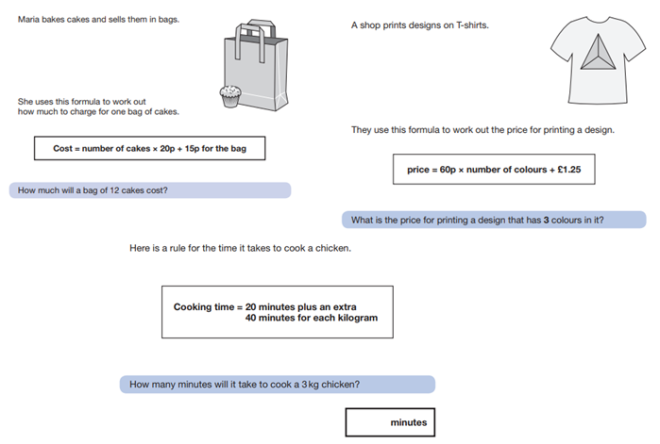
2015 Paper 2 Q20 and 2018 Paper 3 Q16

2017 Paper 3 Q1 and 2016 Paper 2 Q18

2018 Paper 3 Q18 and 2017 Paper 2 Q23

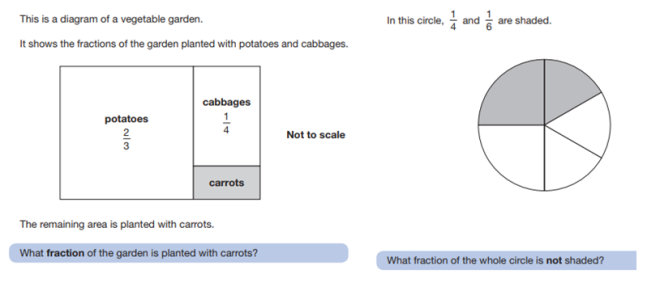
2016 Paper 3 Q11 and 2018 Paper 2 Q15

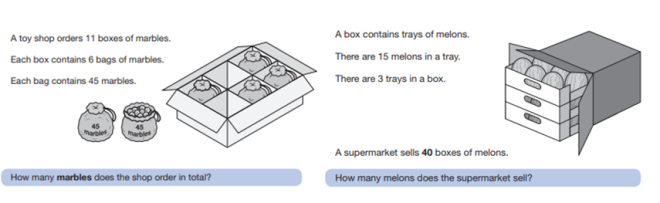
Implications for class practice: children must regularly see past questions when attempting a certain topic to understand the contexts in which it often comes up. This will help to build their understanding of the tests and help them to comprehend them better. To help with this, you can find a lot of the old questions put into short early morning work/starter activities here thanks to @MrCJ248 on Twitter – https://twitter.com/MrCJ248/status/1098346220328767490
NB: There are many more examples of these but this blogpost is long enough as it is! I plan on putting all questions of a similar context into a PowerPoint for teachers to use as a revision session but I haven’t made it yet. It will able available for free on my TES profile – morganell.
To conclude, I will leave you with something that helped me a huge amount last year. @thirdspacetweet compiled together a list of all the maths topics in order of the frequency that they have appeared in recent years. This should help to define your revision sessions more clearly. The picture below was made before the 2018 SATs (can be found here – https://thirdspacelearning.com/blog/how-third-space-learning-teach-maths-2018/). If they do this again for the current SATs, I will update the blog:

Thanks for reading. As usual, if you have any questions contact me on Twitter here  @_mrmorgs

The author

Mr Morgs

Mr Morgs is an experienced Year 6 teacher from South London. He is a trained SATs marker, LA Moderator and has an MA in leadership. He is interested in keeping up-to-date with current educational research, specifically related to the teaching of maths and reading.